Introduction
Many people have been speculating on the probabilities to find a shiny pokemon with the dexnav on pokemon ORAS, but we don't really know actually what are the probabilities. Some analysis based on real encounters gave some results making us think about a 1/200 or 1/300 probability, but this does not really convinced me. So I decided to do some researches about the actual probabilities and the way the game decide if the pokemon is shiny or not.
How a pokemon is considered shiny?
We know every pokemon has a specific PID which is randomly generated when the pokemon itself is generated. The PID is a 32bits value and the pokemon is shiny if (TID xor SID xor PID_high xor PID_low) < 16. So yeah we have a probability of 16/65536 (65536 is the max value for a unsigned 16bits value) so 1/4096.
We know the game can increase the probability with the shiny charm, it computes up to three times the PID if the one generated is not a "shiny one". We can think the dexnav is doing something similar, increasing the number of PID computations, but contrary to what we think the "computation count" is the same as a normal encounter.
How the dexnav could increase the probability?
I investigated how the dexnav is generating the pokemon and before doing anything with the PID, it generates some basic informations that we may see on the bottom screen when we are using the dexnav, such as the pokemon level, id...
These infos are generated and stored in memory before the pokemon is generated, and analysing them I just found out that these infos contain a boolean value for the shininess of the pokemon. When this value is set to 1, the pokemon is automatically shiny and when it is set to 0 then the PID computation is done like for any normal encounter.
So we can think about such a Probability Tree Diagram :
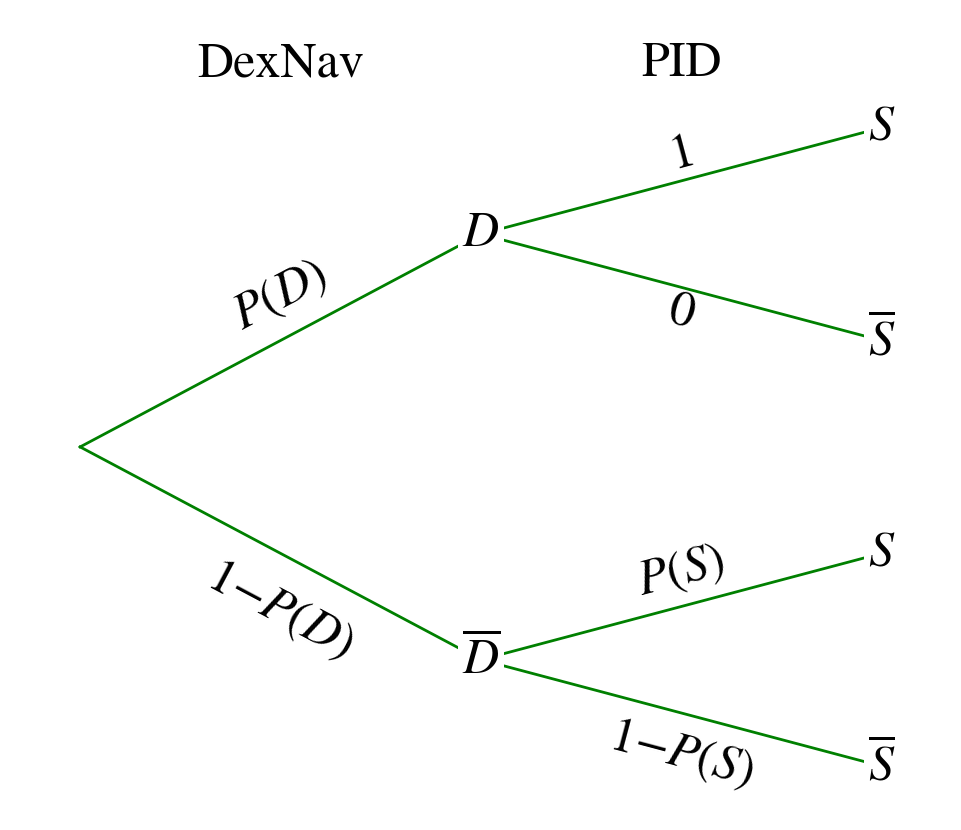
What is the probability that this value is set to 1?
After some researches I found out the algorithm used during the generation to determine if this value is either 1 or 0. This is completely different than the PID generation and computation loop. First the game computes a random 16bits integer value between 0 (included) and 10000 (excluded), so 10000 potential values. Then this value is compared to another one computed before (not random) and if the random value is the smallest then the pokemon is shiny.
So basically it does something like this : if random_value < other_value then shiny=1
Looking how the other value is calculated, I quickly found out it is based on the search level for the current pokemon, and here is the way it is computed :
double other_value = 0.0;
if(level > 200)
{
other_value += level - 200;
level = 200;
}
if(level > 100)
{
other_value += (level * 2) - 200;
level = 100;
}
if(level > 0)
{
other_value += level * 6;
}
other_value *= 0.01;
Now we know how to compute the other value but in fact, like for the PID calculation, the random value and the comparison can be done multiple times.
I will now use the terms dexnav_level instead of "the other value" and "dexnav_random" instead of "the random value". So, like the PID calculation the loop generally iterates once without the charm and three times with the charm, but we may remark that even if the condition is satisfied, the loop is not broken. So you could potentially get multiple "shiny values" at once (this is pointless).
Investigating what could alter the number of iterations, I found out that if the pokemon is going to be the 50th of your dexnav chain the loop iterates 5 more times and if it is going to be the 100th then the loop iterates 10 more times, so let's call this the chain_bonus. Let n be the number of times the loop iterates, we have :
n = 1 + charm_bonus + chain_bonus
with charm_bonus = 0 without the charm and 2 with the charm.
We can now deal with probabilities. Let C be the event : "the condition is satisfied". Since the dexnav_random is an integer and dexnav_level is a floating-point value,
if dexnav_random < dexnav_level then dexnav_random < ceil(dexnav_level)
with ceil(dexnav_level) being the smallest integer that is greater than dexnav_level. There is actually ceil(dexnav_level) values smaller than dexnav_level (and ceil(dexnav_level) because of the dexnav_random being an integer), so we have :
P(C) = ceil(dexnav_level)/10000
So now we are able to compute the probability of C. So let D be the event : "the dexnav boolean value is set to 1 (pokemon shiny because of the dexnav)". D is realized only if C is realized at least once during the multiple loop iterations.
We have a Bernoulli experiment with a success : C is realized, and a failure : C is not realized. We repeat this experiment n times, and count the number X of success. We want to know the probability that C is realized at least once, so :
P(X >= 1) = 1 - P(X = 0)
P(X = 0) = pow(1-P(C), n)
P(X >= 1) = 1 - pow(1-P(C), n)
P(D) = 1 - pow(1-P(C), n)
So we are now able to determine the probability that the pokemon is set shiny during the dexnav generation process, but don't forget our initial probability tree, even if the pokemon isn't set shiny here, it can still be shiny because of the random PID computation.
The final probability
We need to know the probability to have a shiny PID in any case. Without the shiny charm we have the well-known 1/4096, but with the charm the PID is computed 3 times and the loop is broken if a success occurs (when we get a shiny PID). So it is similar to the previous situation but now the process can be interrupted, we repeat up to 3 times and we stop if a success occurs. It can be illustrated by this tree (3 iterations):
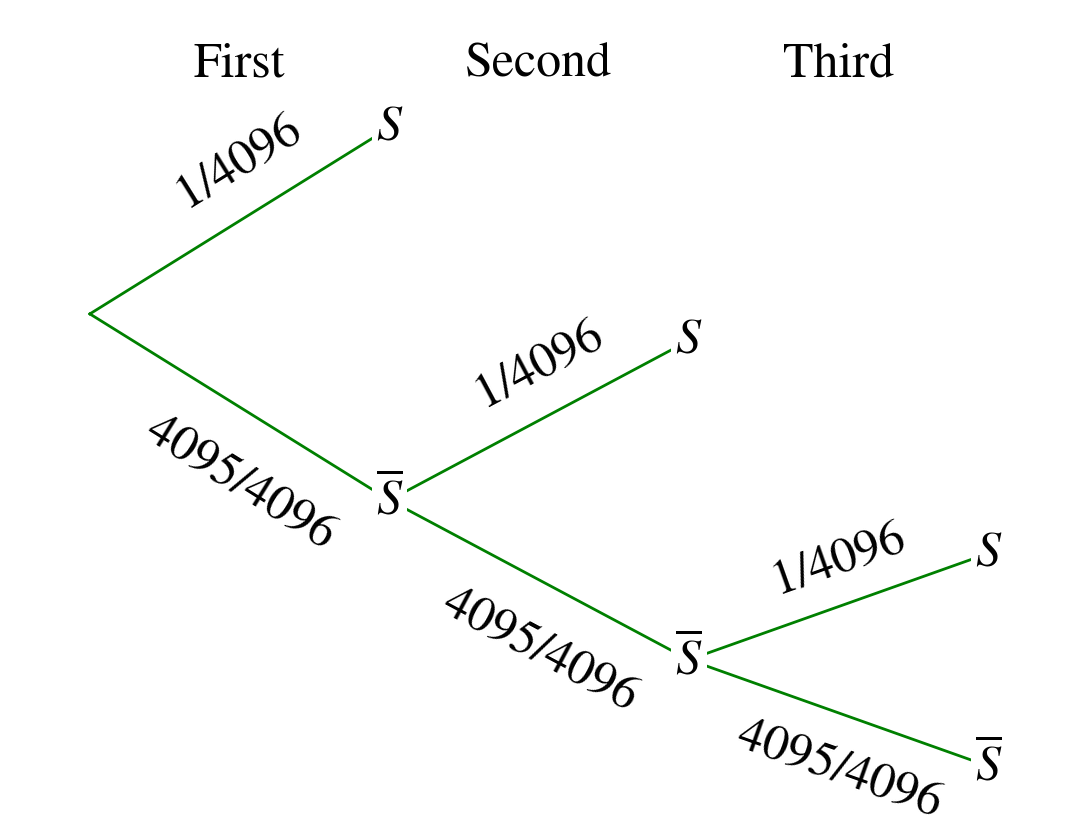
We have X the step for which the success occurs and we consider X=0 if the success do not happen, so we are in the case of a truncated geometric law. Similarly to the previous situation we have :
P(X >= 1) = 1 - P(X = 0)
and
P(X = 0) = pow(4095/4096, n1)
where n1 is the number of iterations, so finally :
P(X >= 1) = 1 - pow(4095/4096, n1)
we have the probability of a shiny PID in any case.
/!\ Some people are saying the probability with the shiny charm is 3/4096 BECAUSE we compute the PID 3 times, SO the probability is multiplied by 3. This is WRONG, actually it is effectively around 3/4096 but it's not because you repeat 3 times the experiment that the probability is multiplied by 3. /!\
So finally, we know all the probabilities necessary to compute the final P(S) :
P(S) = P(D ∩ S) + P(!D ∩ S)
and then :
P(S) = (1 - pow(1-P(C), n)) * 1 + (1 - (1 - pow(1-P(C), n)) * (1 - pow(4095/4096, n1))
so we have :
P(S) = 1 - pow(1-P(C), n) + pow(1-P(C), n) * (1 - pow(4095/4096, n1))
The mysterious value (why I was wrong)
We know how to compute P(S) but I missed a value in the algorithm which after many tests seemed to be permanently equal to 0. But actually it is not always equal to 0 and when it is equal to 1 then n is incremented by 4, so 4 more iterations for the dexnav loop. To decide if this value is set to 1 or 0 the game compute a random 16bits value between 0 (included) and 100(excluded) and if the random value is less than 4, then this specific boolean is set to 1. So basically it does :
if (random < 4) then random_bonus=1
where random_bonus is a boolean value.
So the this is the new tree :
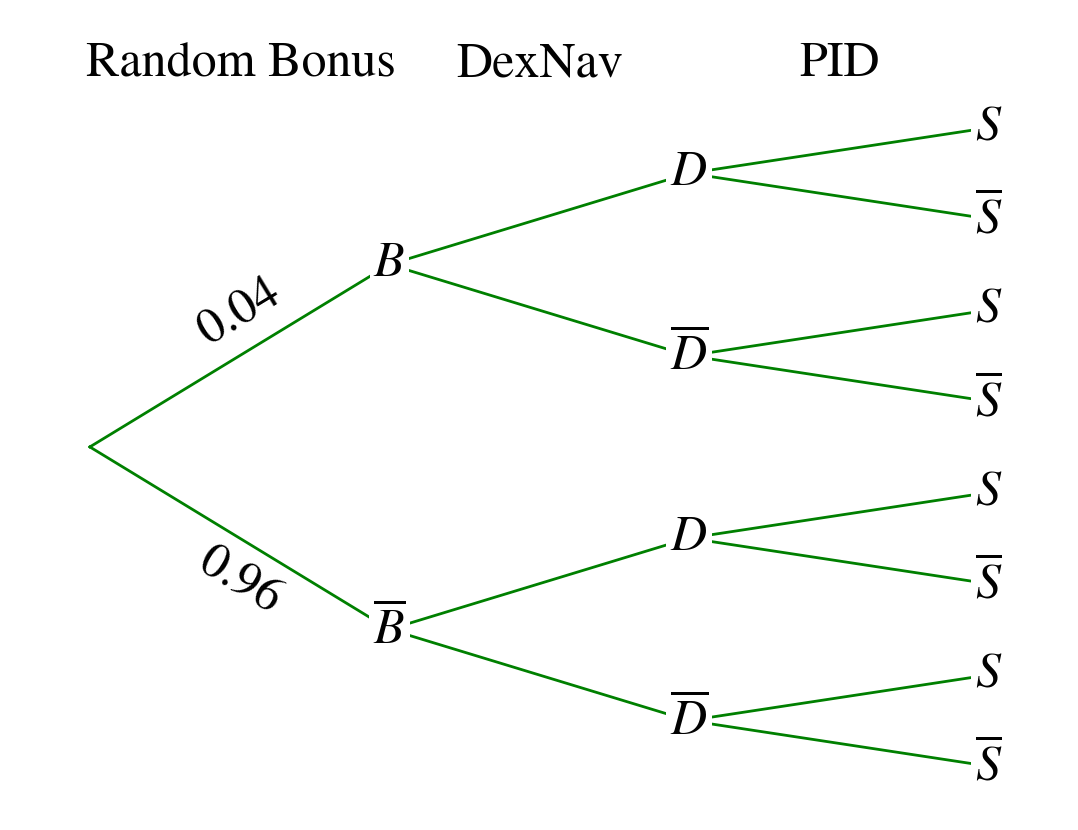
With B the event : "the random bonus is applied". So, now we have :
P(S) = P(B ∩ D ∩ S) + P(B ∩ !D ∩ S) + P(!B ∩ D ∩ S) + P(!B ∩ !D ∩ S)
P(S) = 0.04 * (1 - pow(1-P(C), n+4))
+ 0.04 * pow(1-P(C), n+4) * (1 - pow(4095/4096, n1))
+ 0.96 * (1 - pow(1-P(C), n))
+ 0.96 * pow(1-P(C), n) * (1 - pow(4095/4096, n1))
And n is computed like this :
n = 1 + charm_bonus + chain_bonus;
if(random_value == 1)
n += 4;
Conclusion
We are now able to know what is the probability to find a shiny pokemon, based on the search level, the chain and the shiny charm. If you find a mistake, please open an issue on the corresponding github repo :). I quickly implemented a small calculator, see : 6th gen shiny calculator
If you don't trust me, please look at the related disassembly part from the game binaries: PROOF